Linear Algebra and Learning from Data(3)

Introduction

1.5 Orthogonal Matrices and Subspaces

우리가 일반적으로 알고 있는 직교(orthogonal)라는 단어는 두 벡터 사이의 관계 중 하나지만 이것을 확장하려고 한다.

1. 두 벡터 $\mathbf{x},\mathbf{y}$가 orthogonal

$\mathbf{x}^T\mathbf{y}=0$ (in real), $\overline{\mathbf{x}}^T\mathbf{y}=0$ (in complex)

2. Orthogonal basis of subspaces

$\forall \mathbf{v}_i,\mathbf{v}_j\in {\rm Basis}, \mathbf{v}_i^T\mathbf{v}_j=0$ if $\mathbf{v}_i^T\mathbf{v}_i=1$ for all $i$, it is called orthonormal basis.

3. Subspaces $R$과 $N$이 orthogonal

$\forall \mathbf{x}\in R,\, \forall \mathbf{y}\in N,\, \mathbf{x}^T\mathbf{y}=0$

2의 orthonormal basis의 일부를 열로 가지는 행렬$Q$를 생각해보자.

4. $Q^TQ=I$

$\| Q\mathbf{x} \| = \| \mathbf{x} \|$가 된다. $(\because (Q\mathbf{x})^T(Q\mathbf{x})=\mathbf{x}^T Q^T Q \mathbf{x}=\mathbf{x}^T\mathbf{x})$

이제 orthonormal basis의 전부를 열로 가지는 행렬$Q$을 생각해보자.

5. Orthogonal matrices

$Q^TQ=QQ^T=I$ $(\because (Q^TQ)^T=QQ^T=I \Rightarrow Q^T=Q^{-1})$

orthogonal objects의 Example을 몇 개 살펴보자.

Examples

Example of Orthogonal basis

아다마르 행렬(Hadamard matrices) 아다마르 행렬은 모든 원소가 $1,-1$이고, 행벡터와 열벡터들이 각각 orthogoanl한 행렬이다. 예시를 하나 들어보자.

\[ H_2=\begin{bmatrix} 1 & 1 \cr 1 & -1 \end{bmatrix} \]

$H_2$의 모든 행과 열은 각각 $\mathbb{R}^2$위에서 orthogonal이다. $H_2$를 만들었다면 $H_4$는 더 쉽게 만들 수 있다.

\[ H_4=\begin{bmatrix} H_2 & H_2 \cr H_2 & -H_2 \end{bmatrix} \]

$n\times n$크기의 아다마르 행렬이 존재할 필요충분조건을 찾는 문제는 아직까지 풀리지 않은 난제중 하나이다.

베르누이 행렬(bernoulli matrix) 문제 베르누이 행렬은 아다마르 행렬과 비슷하게 모든 성문이 $1,-1$인 행렬이다. 사실 아다마르 행렬이 특별한 베르누이 행렬이다.

이 베르누이 행렬에 대해서도 풀리지 않은 난제가 있다. 무작위 $n\times n$ 베르누이 행렬의 열공간이 $\mathbb{R}^{n-1}$의 부분공간이 될 확률을 구하는 것이다.

$2$차원 공간 $\mathbb{R}^2$를 생각해보자. 모든 가능한 벡터는 다음과 같다.

\[\begin{bmatrix} 1 & 1 \end{bmatrix},\begin{bmatrix} 1 & -1 \end{bmatrix},\begin{bmatrix} -1 & 1 \end{bmatrix},\begin{bmatrix} -1 & -1 \end{bmatrix}\]

$4$개의 벡터중 무작위로 $2$개를 뽑았을 때 두 벡터가 independence할 확률은 $\frac{1}{2}$이다.

이제 $3$차원 공간 $\mathbb{R}^3$을 생각해보자. 모든 가능한 벡터는 다음과 같다.

\[\begin{bmatrix} 1 & 1 & 1 \end{bmatrix},\begin{bmatrix} 1 & 1 & -1 \end{bmatrix},\begin{bmatrix} 1 & -1 & 1 \end{bmatrix},\begin{bmatrix} 1 & -1 & -1 \end{bmatrix},\] \[\begin{bmatrix} -1 & 1 & 1 \end{bmatrix},\begin{bmatrix} -1 & 1 & 1 \end{bmatrix},\begin{bmatrix} -1 & 1 & -1 \end{bmatrix},\begin{bmatrix} -1 & -1 & -1 \end{bmatrix}\]

$8$개의 벡터중 무작위로 $3$개를 뽑았을 때 세 벡터가 모두 indepencence할 확률을 계산하면 $\frac{5}{8}$이다. $n$차원 공간에서는 어떨까?

Example of Orthogonal subspaces

Linear algebra의 The Big picture을 떠올려보자.

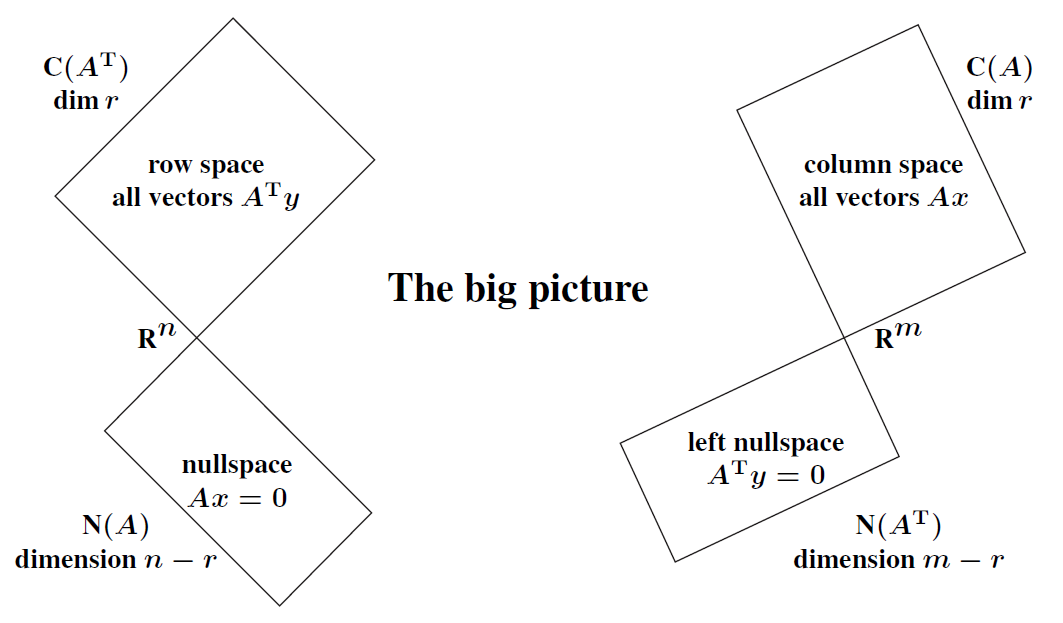
행공간과 영공간이 orthogonal하다는 것을 보이자.

행렬 방정식 $A\mathbf{x}=\mathbf{0}$를 생각해보자.

$A$의 모든 행과 영공간의 벡터가 곱해져서 $0$이 된다. 즉, A의 각 행은 영공간과 orthogonal하다. 따라서 행공간과 영공간이 orthogonal하다.

비슷하게 열공간과 좌영공간이 orthogonal하다는 것 또한 쉽게 보일 수 있다.

앞선 글에서 $A\mathbf{x}=\mathbf{b}$가 해가 존재하기 위해서는 $\mathbf{b}$가 $A$의 열공간 안에 있어야 한다고 설명했다. 이 개념을 The Big picture에 추가해주면 다음과 같은 그림이 된다.

여기서 SVD와 연결된다. SVD는 데이터 과학에서 가장 중요한 정리중 하나로, $A$의 행공간에서 orthogonal basis $\mathbf{v}_1,\ldots,\mathbf{v}_r$을 찾고, 열공간에서 $\mathbf{u}_1,\ldots,\mathbf{u}_r$을 찾는다.

Singular vectors

singular value & singular vector
$A\mathbf{v}_1 = \sigma_1\mathbf{u}_1, A\mathbf{v}_2 = \sigma_2\mathbf{u}_2, \ldots , A\mathbf{v}_r = \sigma_r\mathbf{u}_r$

$A$의 행공간의 orthogonal basis는 $A$의 열공간의 orthogonal basis와 $A$를 통해서 연결된다.