Linear Algebra and Learning from Data(2)

Updated: July 22, 2020

여러 수학에는 기본정리라고 불리는 여러 중요한 정리들이 있다.

대표적인 기본정리로는 미적분학 기본정리(fundamental theorem of calculus), 대수학의 기본정리(fundamental theorem of algebra)등이 있다.

그렇다면 선형대수학의 기본정리라고 부를 수 있는 중요한 정리는 무엇이 있을까?

Introduction

이 절에서는 Starng 교수님이 계속 강조하는 선형대수학의 $4$가지 부분공간에 대해서 다루고 있다.

열공간(column space) $\mathbf{C}(A)$ $A$의 열의 모든 일차 결합
행공간(row space) $\mathbf{C}(A^T)$ $A^T$의 열의 모든 일차 결합
영공간(nullspace) $\mathbf{N}(A)$ $A\mathbf{x}=0$의 모든 해 $\mathbf{x}$
좌영공간(left nullspace) $\mathbf{N}(A^T)$ $A^T\mathbf{y}=0$의 모든 해 $\mathbf{y}$

간단한 Example을 통해서 이 부분공간들의 concept과 이 공간들이 왜 중요한지에 대해서 이해해보자.

\[A=\begin{bmatrix}1&2\cr 3&6\end{bmatrix}=\mathbf{uv}^T\]

모든 부분공간들은 $\mathbb{R}^2$의 부분공간이다.

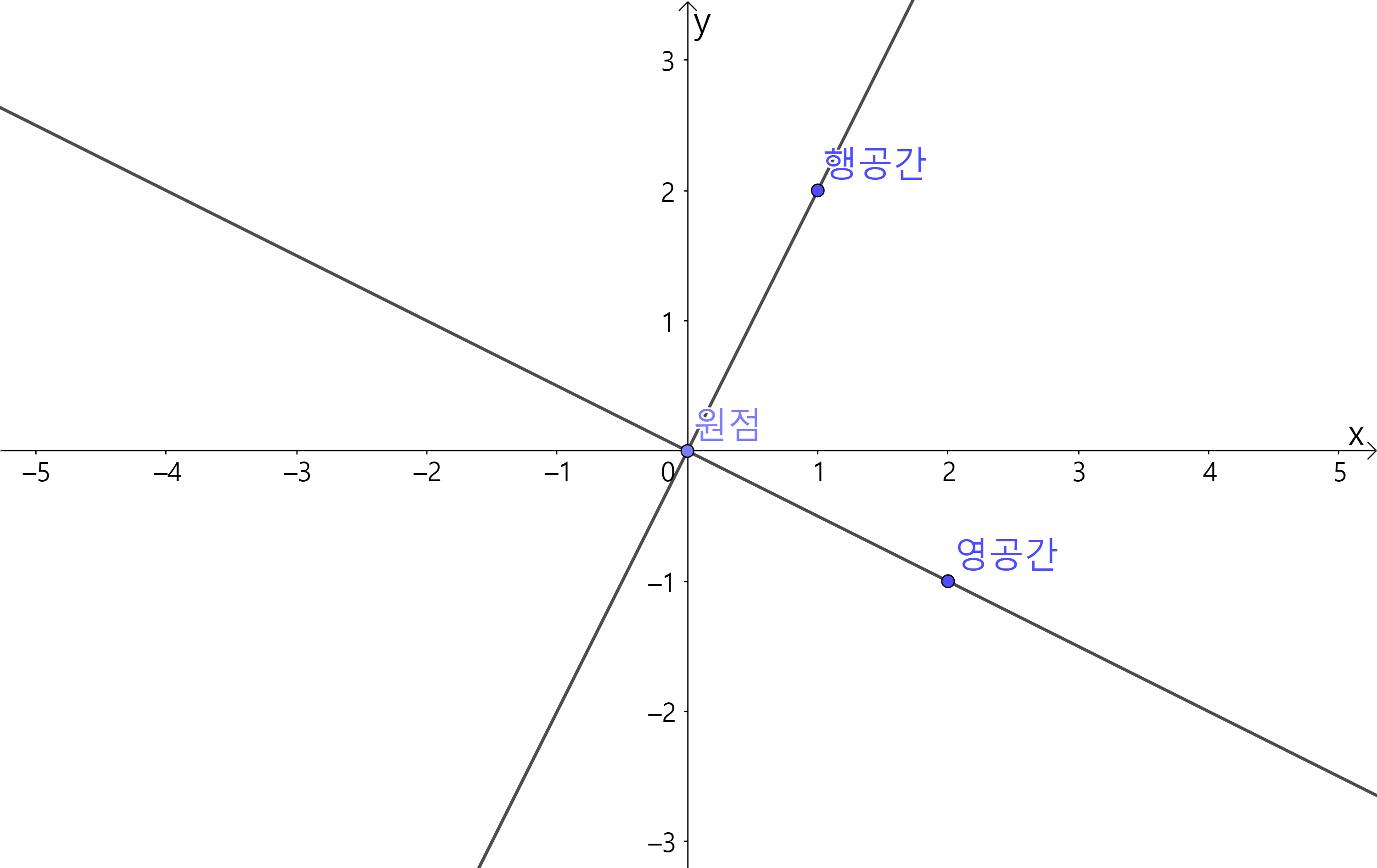
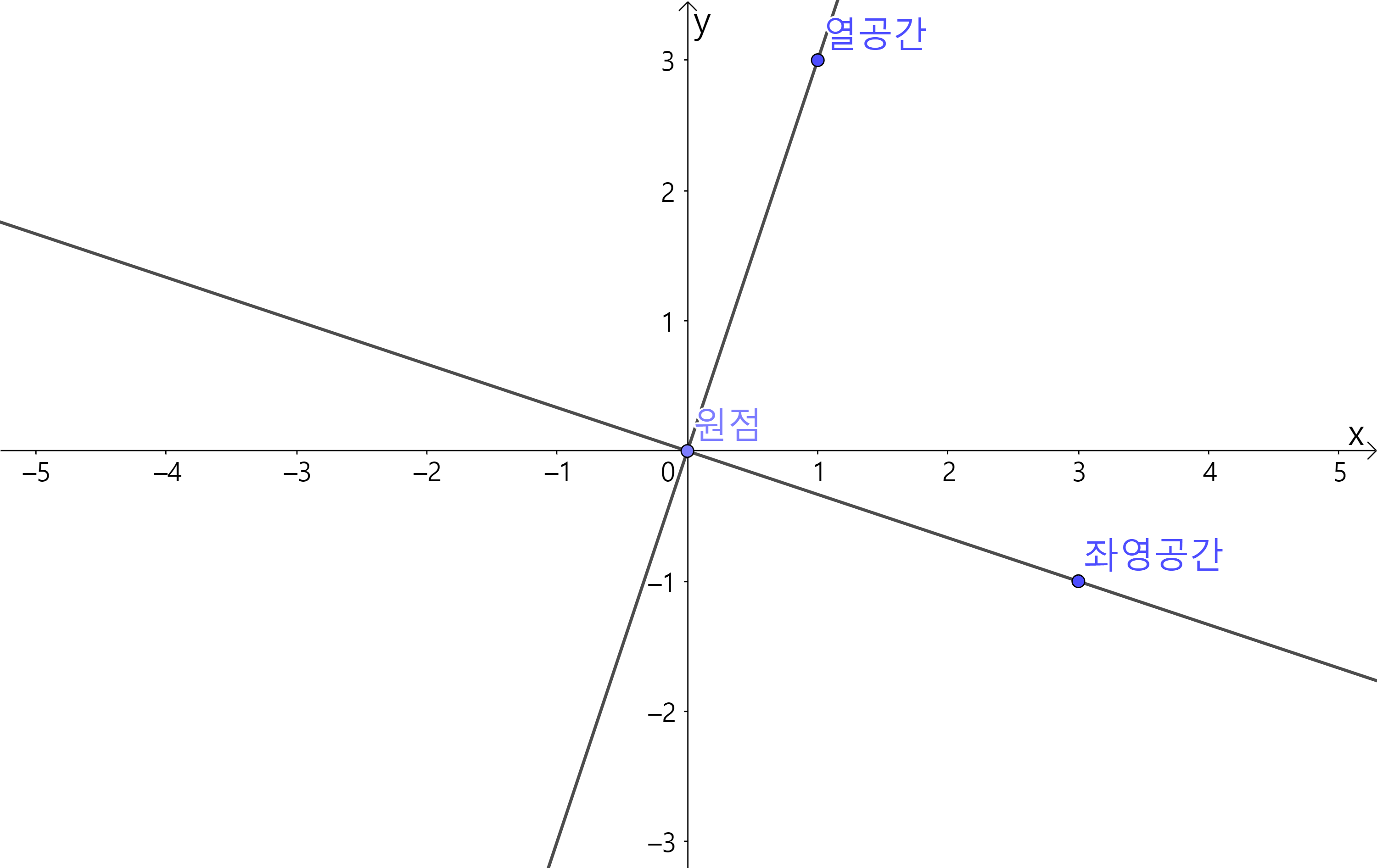
$\mathbf{C}(A)$는 원점과 $\mathbf{u}=\begin{bmatrix} 1 \cr 3 \end{bmatrix}$을 지나는 직선
$\mathbf{C}(A^T)$는 원점과 $\mathbf{u}=\begin{bmatrix} 1 \cr 2 \end{bmatrix}$을 지나는 직선
$\mathbf{N}(A)$는 원점과 $\mathbf{u}=\begin{bmatrix} 2 \cr -1 \end{bmatrix}$을 지나는 직선
$\mathbf{N}(A^T)$는 원점과 $\mathbf{u}=\begin{bmatrix} 3 \cr -1 \end{bmatrix}$을 지나는 직선

우리는 이 벡터들중 두 쌍이 직교한다는 것을 쉽게 알 수 있다.


$\mathbf{C}(A^T)$와 $\mathbf{N}(A)$는 직교한다.	$\mathbf{C}(A)$와 $\mathbf{N}(A^T)$는 직교한다.

행렬의 크기가 커져도(차원이 높아져도) 여전히 이 관계가 성립할 것인가? 답은 그렇다!

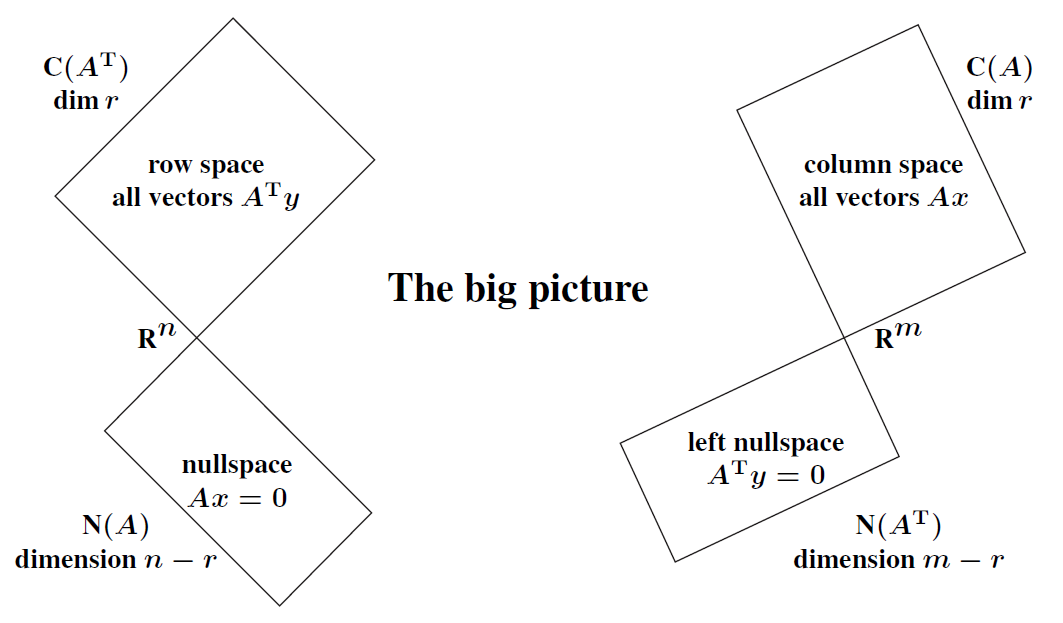
심지어 $A$가 $m\times n$ 행렬일 때, 각 부분공간의 차원은 다음과 같은 관계를 가진다.

\[\mathrm{dim}(\mathbf{C}(A^T))+\mathrm{dim}(\mathbf{N}(A))=n\]

\[\mathrm{dim}(\mathbf{C}(A))+\mathrm{dim}(\mathbf{N}(A^T))=m\]

이것을 선형대수학의 The Big Picture라고 한다.

선형대수학 시간에서 우리는 $\det (AB)=\det (A) \det(B)$는 성립하지만 $\det (A+B)=\det (A)+\det(B)$는 아니라는 것을 배웠을 것이다. 그렇다면 행렬의 랭크는 어떨까?

행렬들 $A,B, AB, A+B$의 랭크는 다음 관계를 가진다.