Transition probability tensor of a higher-order Markov chain

0. TENSOR

일반적으로 텐서(tensor) $\mathscr{A}=(a_{i_{1}\cdots i_{m}})$는 $a_{i_{1}\cdots i_{m}}\in \mathbf{F}:\textrm{field}$ where $i_{j}=1,\ldots,n_{j},\textrm{ for }j=1,\ldots,m$인 multi-array이다.

우리가 잘 아는 matrix로 예로 들어보자.

\[ A = \begin{bmatrix} 1 & 2 & 3 \cr 4 & 5 & 6 \end{bmatrix} \]

Matrix $A=(a_{i_{1}i_{2}})$는 $i_1=1,2$, $i_2=1,2,3$ 인 텐서이다.

여기서 $m$은 텐서의 위수(order)이고, $(n_1,\ldots,n_m)$은 텐서의 차원(dimension)이다.

행렬 $A$의 크기가 $2\times 3=6$인 것 처럼, tensor $\mathscr{A}$의 크기(size)는 $n_1\times \cdots \times n_m$이다.

만약 $n_1=\cdots = n_m$이면, $\mathscr{A}$는 $m$th order $n$-dimensional tensor라고 한다.

그리고 $m$th order $n$-dimensional real tensor을 모두 모은 집합을 $T_{m,n}$라고 한다.

1. INTRODUCTION

미래를 예측하는 것은 언제나 인간이 가장 하고 싶어하는 일이다. 유효한 방법 중 하나가 바로 Markov chain을 사용하는 것이다. 그리고 쉽게 찾아볼 수 있는 Markov chain의 응용은 대부분 First-order Markov chains이다. 좋은 정리들이 이미 잘 연구되어있기도 할 뿐더러, 이 정리들은 아직 higher-order Markov chains로 확장되어 연구되지 않았다. 혹은 할 수 없거나. 때문에 higher-order Markov chains은 First-order Markov chains로 근사되어 종종 사용되어 왔다. Tensor, 특히 nonnegative tensor가 higher-order Markov chains과 연관지을 수 있다는 사실은 쉽게 알 수 있다. 한편, tensor multiplication은 tensor와 vector, 혹은 tensor와 matrix와의 multiplicaiton은 많았지만, tensor와 tensor의 곱에 대해서는 많은 연구가 이루어지고 있지 않았다. 본 연구에서는 tensor와 tensor의 multiplication을 하나 정의하고, 이 multiplication이 higher-order Markov chains과 어떤 조화를 이루는지 살펴볼 것이다.

1.1. Markov chains

우리는 Matrix가 First-order Markov chains과 깊은 관련이 있다는 것을 충분히 알고 있다. First-order Markov chains과 transition matrix의 정의를 다시 짚고 넘어가자.

Definition 1

Suppose $\{X_n \}, n\in \mathbb{Z},$ is a sequence of stochastic functions with the same probability distribution and $i_j \in S$($S$ is state space) such that \[ P(X_n = i_n| X_{n-1} = i_{n-1}, X_{n-2} = i_{n-2},\ldots X_0 = i_0) = P(X_n = i_n | X_{n-1}=i_{n-1}) \] then we call $\{X_n\}$ a first-order Markov chain.

Let $p(x,y) = P(X_n = x| X_{n-1} = y)$, $p^n(x,y) = P(X_n = x| X_0 = y)$ and call $p$ a transition probability matrix.

예를 들면, 다음과 같은 first-order Markov chain이 있다고 하자.

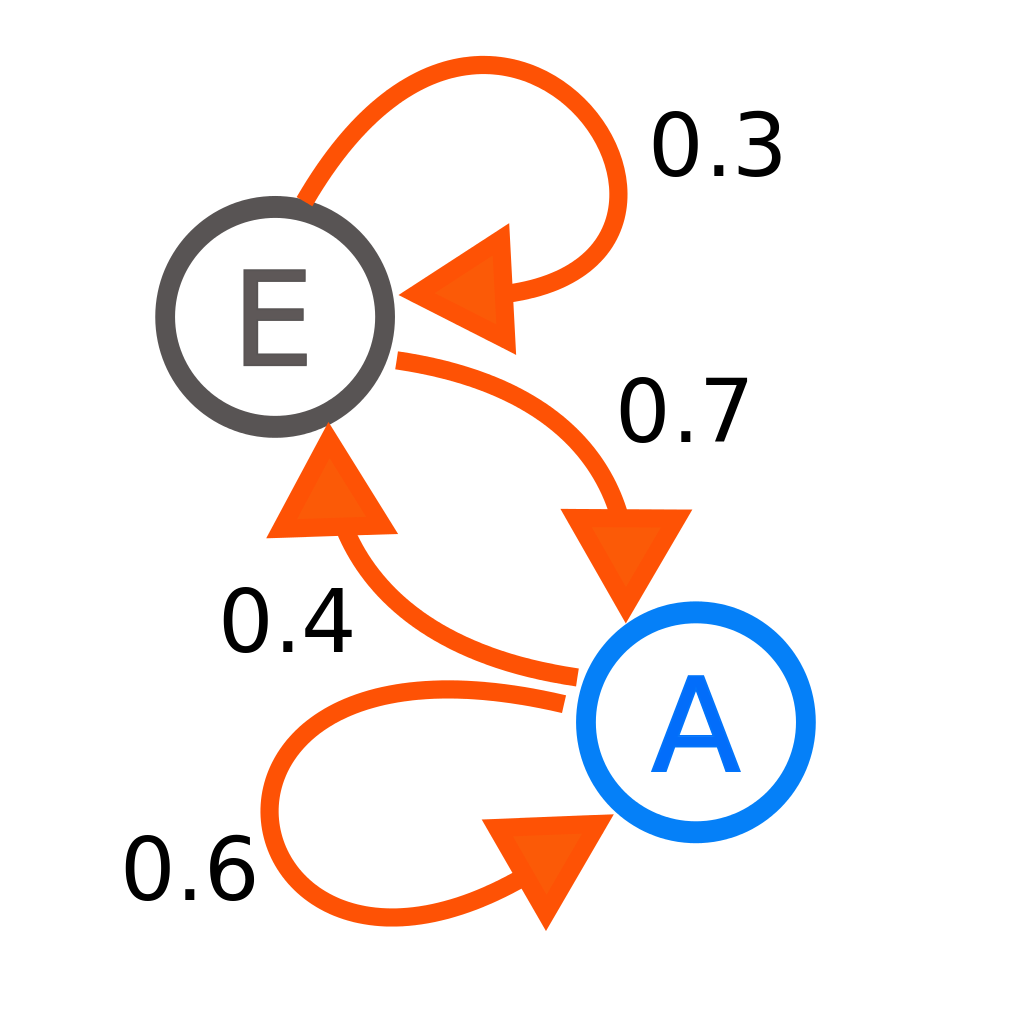
그렇다면 이 Markov chain에 대한 transition matrix는 다음과 같다.

\[ \begin{array}{cc} & \begin{array}{cc} E & A \end{array} \cr \begin{array}{c} E \cr A \end{array} & \left[\begin{array}{cc} 0.3 & 0.7 \cr 0.4 & 0.6 \end{array} \right] \end{array} \begin{array}{c} \cr =p \end{array} \]

Theorem 1 (Chapman–Kolmogorov equation)

Let $\{X_n \}$ be a first-order Markov chain and $m,n \in \mathbb{N}$, then \[ p^{m+n}(x,y) = \sum\limits_{k\in S}p^m(x,k) p^n(k,y) \]

이 정리를 통해서 first-order Markov chain에 대한 transition matrix와 행렬 곱의 유용성을 알 수 있다.

다음은 transition matrix에 대한 stationary distribution의 정의이다.

Definition 2

Assume that $\{X_n \}$ is a first-order Markov chain, $|S | = n$, $p$ is its transition matrix and $\pi$ is a non-negative $n$-dimensional vector with $\sum\limits_{x\in S} \pi (x) = 1$. We call $\pi$ a stationary distribution for $\{X_n \}$ if \[ p \pi = \pi \]

위 식을 통해서 $\pi$가 $p$의 고윳값 $1$일 때 그에 대응되는 고유벡터라는 것을 쉽게 알 수 있다.

다음 두 정리는 first-order Markov chain의 $p$와 $\pi$의 관계에 대한 정리들이다.

Theorem 2

If $p$ is an irreducible transition probability matrix for the first-order Markov chain $\{X_n \}$, then there exists a unique positive stationary distribution for $\{X_n \}$.

Theorem 3 (Convergence theorem)

Let $p$ be an irreducible, aperiodic, and has stationary distribution $\pi$ then for every $y$ in state space \[ \lim\limits_{n\rightarrow \infty} p^n(x,y) = \pi (x) \]

$p$가 non-negative라는 것은 쉽게 알 수 있다. $p$의 $0$보다 큰 원소를 모두 $1$로 만들고 이것을 $G_p$라고 하자. 이러한 경우 irreducible은 $G_p$의 어떤 state에서도 다른 state로 도달할 수 있는 상태를 말한다. 예를 들면 다음과 같은 directed graph를 생각해보자.

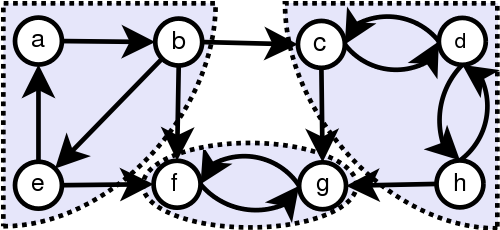
표시된 영역 안의 점들은, 영역안의 다른 모든 점들로 갈 수 있다. (예: $a\rightarrow b \rightarrow e$) 이러한 상태를 strongly connected라고 한다.

그리고 $p$가 periodic하다 것은 일정한 주기 $t$에 대해서 반드시 state로 돌아오는 주기가 있을 때를 말하고 그렇지 않을 때 $p$가 aperiodic하다고 한다.

1.2. Tensors and higher-order Markov chains

다음은 우리에게 익숙한 Tensor와 vector간의 $k$-mode product에서 파생된 정의이다.

Definition 3

Suppose that $\mathscr{A} = (a_{i_1 i_2 \cdots i_m}) \in T_{m,n}$ and $x = (x_1,x_2,\ldots,x_n)^T$ is an $n$-dimensional vector, then

\[( \mathscr{A} x^{m-1} ) = \sum\limits_{i_2, \ldots ,i_m=1}^{n} a_{i_1 i_2 \cdots i_m} \times x_{i_2} \times \cdots \times x_{i_m} \]

Definition 4

An $(m-1)$-order Markov chain is a sequence of stochastic functions that has the following property \[ \begin{aligned} & P(X_n = i_n | X_{n-1} = i_{n-1}, X_{n-2} = i_{n-2}, \ldots , X_{0} = i_{0}) \cr & = P(X_n = i_n | X_{n-1} = i_{n-1}, X_{n-2} = i_{n-2}, \ldots , X_{n-m+1} = i_{n-m+1}) \end{aligned} \]

우리는 $(m-1)$-order Markov chain의 transition tensor를 transition matrix와 비슷하게 다음과 같이 정의할 수 있다.

\[ \begin{aligned} & p(i_{n}, i_{n-1}, \ldots ,i_{n-m+1}) \cr & = P(X_n = i_n | X_{n-1} = i_{n-1}, X_{n-2} = i_{n-2}, \ldots , X_{n-m+1} = i_{n-m+1}) \end{aligned} \]

$m=2$로 두게 되면 first-order Markov chain이 된다는 것을 쉽게 알 수 있다.

MAIN RESULT

2.1. Product for transition probability tensors

이 section에서는 새로운 tensor product를 정의하고 그것의 성질에 대하여 살펴본다.

Definition 5

Suppose we have a transition probability tensor such as $p$ for an $(m-1)$-order Markov chain, then we define its second power as

\[ \begin{aligned} & p^2 (i_{n}, i_{n-1}, i_{n-2}, \ldots ,i_{n-m+1}) \cr & = \sum\limits_{k} p (i_{n}, k, i_{n-2}, \ldots ,i_{n-m}) p (k, i_{n-1}, i_{n-2}, \ldots ,i_{n-m+1}) \end{aligned} \]

이 정의로부터 우리는 다음 사실을 바로 알 수 있다.

Proposition 1

If $p$ is a transition probability tensor for an $(m-1)$-order Markov chain, then we have

\[ \begin{aligned} & p^2 (i_{n}, i_{n-1}, i_{n-2}, \ldots ,i_{n-m+1}) \cr & = \sum\limits_{k} p (i_{n}, k, i_{n-1}, \ldots ,i_{n-m}) p (k, i_{n-1}, i_{n-2}, \ldots ,i_{n-m+1}) \cr & = P(X_n = i_n | X_{n-2} = i_{n-1}, X_{n-3} = i_{n-2}, \ldots , X_{n-m+1} = i_{n-m}) \end{aligned} \]

in which summations are taking place over the state space of the Markov chain.

proof

조건부 확률의 정의를 사용하면 쉽게 증명할 수 있다.

\[ \begin{aligned} P(X_n =& i_n, X_{n-1} = k | X_{n-2} = i_{n-1}, X_{n-3} = i_{n-2}, \ldots , X_{n-m} = i_{n-m+1}) \cr =& \frac{P(X_n = i_n, X_{n-1} = k, X_{n-2} = i_{n-1}, X_{n-3} = i_{n-2}, \ldots , X_{n-m} = i_{n-m+1})}{P( X_{n-2} = i_{n-1}, X_{n-3} = i_{n-2}, \ldots , X_{n-m} = i_{n-m+1})} \cr =& \frac{P(X_n = i_n, X_{n-1} = k, X_{n-2} = i_{n-1}, X_{n-3} = i_{n-2}, \ldots , X_{n-m} = i_{n-m+1})}{P( X_{n-1} = k, X_{n-2} = i_{n-1}, \ldots , X_{n-m} = i_{n-m+1})} \cr & \times \frac{P( X_{n-1} = k, X_{n-2} = i_{n-1}, \ldots , X_{n-m} = i_{n-m+1})}{P( X_{n-2} = i_{n-1}, X_{n-3} = i_{n-2}, \ldots , X_{n-m} = i_{n-m+1})} \cr =& P(X_n = i_n | X_{n-1} = k, X_{n-2} = i_{n-1}, X_{n-3} = i_{n-2}, \ldots , X_{n-m} = i_{n-m+1}) \cr & \times P(X_{n-1} = k | X_{n-2} = i_{n-1}, X_{n-3} = i_{n-2}, \ldots , X_{n-m} = i_{n-m+1}) \cr =& P(X_n = i_n | X_{n-1} = k, X_{n-2} = i_{n-1}, X_{n-3} = i_{n-2}, \ldots , X_{n-m+1} = i_{n-m}) \cr & \times P(X_{n-1} = k | X_{n-2} = i_{n-1}, X_{n-3} = i_{n-2}, \ldots , X_{n-m} = i_{n-m+1}) \cr =& p (i_{n}, k, i_{n-1}, \ldots ,i_{n-m}) p (k, i_{n-1}, i_{n-2}, \ldots ,i_{n-m+1}) \end{aligned}
\]

따라서

\[ \begin{aligned} & P(X_n = i_n | X_{n-2} = i_{n-1}, X_{n-3} = i_{n-2}, \ldots , X_{n-m+1} = i_{n-m}) \cr &= \sum\limits_{k} P(X_n = i_n, X_{n-1} = k | X_{n-2} = i_{n-1}, X_{n-3} = i_{n-2}, \ldots , X_{n-m} = i_{n-m+1}) \cr &= \sum\limits_{k} p (i_{n}, k, i_{n-1}, \ldots ,i_{n-m}) p (k, i_{n-1}, i_{n-2}, \ldots ,i_{n-m+1}) \end{aligned}
\]

$\blacksquare$

proposition을 통해서 세 제곱이 어떻게 될지는 쉽게 알 수 있다.

Corollary 1

If $p$ is a transition probability tensor for an $(m-1)$-order Markov chain, then we have

\[ \begin{aligned} & p^3 (i_{n}, i_{n-1}, i_{n-2}, \ldots ,i_{n-m+1}) \cr =& \sum\limits_{k_2} p^2 (i_{n}, k_2, i_{n-1}, \ldots ,i_{n-m}) p (k_2, i_{n-1}, i_{n-2}, \ldots ,i_{n-m+1}) \cr =& \sum\limits_{k_1} \sum\limits_{k_2} p(i_n, k_1, k_2 ,i_{n-1}, \ldots , i_{n-m+1}) p(k_1, k_2, i_{n-1},\ldots ,i_{n-m}) p(k_2, i_{n-1}, i_{n-2}, \ldots ,i_{n-m+1}) \end{aligned}
\]

좀 더 높은 거듭제곱에서는 어떨까? Corollary 1을 일반화 하면 다음 Corollary를 얻을 수 있다.

Corollary 2

If $p$ is a transition probability tensor for an $(m-1)$-order Markov chain, then we have

\[ \begin{aligned} & P(X_n = i_n | X_{0} = i_{n-1}, X_{-1} = i_{n-2}, \ldots , X_{2-m} = i_{n-m+1}) \cr =& p^n (i_{n}, i_{n-1}, i_{n-2}, \ldots ,i_{n-m+1}) \cr =& \sum\limits_{k_2} p^{n-1} (i_{n}, k_2, i_{n-1}, \ldots ,i_{n-m}) p (k_2, i_{n-1}, i_{n-2}, \ldots ,i_{n-m+1}) \end{aligned}
\]

$m>3$이라고 하자. 우리는 transition probability tensor $p$의 거듭제곱에 대해서는 정의했지만 $m>3$일 때 $(m-1)$-order Markov chain에 대해서 Chapman–Kolmogorov equation이 더이상 성립하지 않는다는 것을 알 수 있다. 대신 다음 정리가 성립한다.

Theorem 4

If $p$ is a transition probability tensor for an $(m-1)$-order Markov chain, then for any $n,l\in \mathbb{N}$

\[ \begin{aligned} &p^{l+n}(i_{n}, i_{n-1}, i_{n-2}, \ldots ,i_{n-m+1}) \cr =& \sum\limits_{k_{1}, k_{2}, \ldots ,k_{m-1}} p^{l} (i_{n}, k_{1}, k_{2}, \ldots ,k_{m-1}) \cr &\times P(X_n = k_1 , X_{n-1} = k_2 ,\ldots, X_{n-m+1} = k_{m-2} | X_{m-n} = k_{m-1}, X_{-m-1} = i_{n-1}, \ldots , X_{-2m-1}=i_{n-m+1} ) \cr &\times p^{n-m} (k_{m-1},i_{n-1},i_{n-2},\ldots , i_{n-m+1}) \end{aligned} \]

proof

Theorem 5

If $p$ is a transition probability tensor for an $(m-1)$-order Markov chain, then for any $k,n,l\in \mathbb{N}$ which $l>m$, we have

\[ \begin{aligned} &p^{l+n+k}(i_{n}, i_{n-1}, i_{n-2}, \ldots ,i_{n-m+1}) \cr =& \sum\limits_{k_{1}, k_{2}, \ldots ,k_{m-1}} p^{k} (i_{n}, k_{1}, k_{2}, \ldots ,k_{m-1}) \cr &\times p^{l} (k_{l+1}, i_{n-1}, \ldots, i_{n-m+1}) \cr &\times P(X_{n+l} = k_1 , X_{n-1} = k_2 ,\ldots, X_{n-1} = k_{l} | X_{n} = k_{l+1}, X_{0} = i_{n-1}, \ldots , X_{-m+2}=i_{n-m+1} ) \end{aligned} \]

proof